[resending this with smaller images as first try didn't pass mailing list server]
On 22/10/13 22:42, Markus Metz wrote:
Moritz Lennert wrote:
Markus M,
I know this is still very fresh, but I was excited about seeing your
addition to v.voronoi allowing to calculate skeletons and longest lines for
areas. Amongst others, this could be useful for calculating some shape
parameters of polygons for region-based classification.
So, just a quick feedback. I ran the module on the entire urbanarea map, in
order to test scalability. The results are really nice and I haven't found
evident errors, yet.
I found evident errors in some other test data. The voronoi algorithm
suffers from problems related to floating point representation errors,
also sometimes apparent when calculating voronoi diagrams for areas.
It takes quite a while, though:
Yes, because it is a brute force approach. The problem of finding the
center line for areas, or an area skeleton from which the center line
can be extracted, must have been solved previously. A literature
research might help. On first glance, I did not find a solution,
though. Only for straight skeletons which are not suitable to extract
a center line.
I found a few articles that seem interesting to my lay eyes. I'll send them to you off-list.
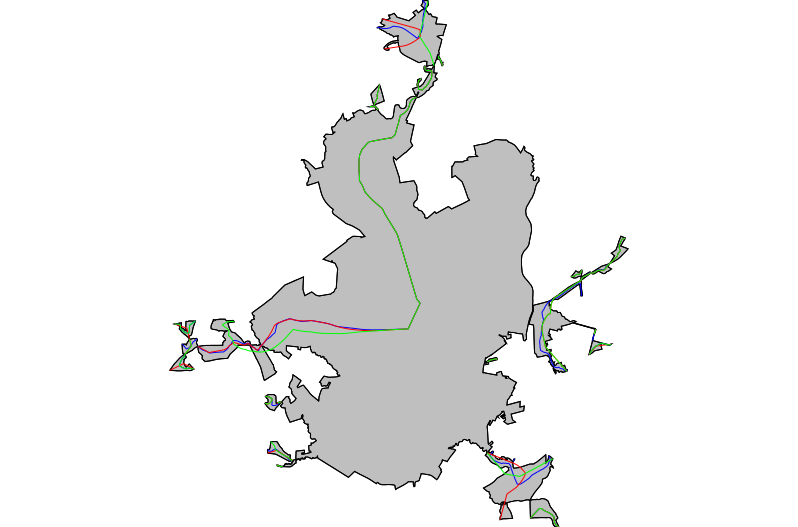
I've done a bit of experimentation with generalisation (see comp_area_generalisation.png for the resulting areas):
v.extract urbanarea out=myarea cats=93
g.region vect=myarea res=500 -a
time v.generalize input=myarea@user1 output=myarea_general method=douglas threshold=1000 --o
real 0m0.060s
user 0m0.036s
sys 0m0.012s
time v.voronoi -s input=myarea@user1 output=skeleton thin=2000
real 1m13.463s
user 1m13.040s
sys 0m0.392s
time v.voronoi -s input=myarea_general output=skeleton_general thin=2000
real 0m29.660s
user 0m29.468s
sys 0m0.180s
i.e. in terms of real time 1m13s vs 30s
The skeleton is not _that_ different (see attached image, blue=without generalisation, red=with generalisation) and is probably sufficient for many use cases.
And for the center line:
time v.voronoi -s input=myarea@user1 output=centerline thin=-1
real 1m14.255s
user 1m13.732s
sys 0m0.376s
Length of center line: 96202m
time v.voronoi -s input=myarea_general output=centerline_general thin=-1
real 0m29.230s
user 0m29.076s
sys 0m0.144s
Length of center line: 91979m
i.e. same proportions as for the skeleton, and again the difference is probably not so significant as to make the result unusable.
Pushing generalisation a bit further:
time v.generalize input=myarea@user1 output=myarea_general2000 method=douglas threshold=2000
real 0m0.052s
user 0m0.032s
sys 0m0.012s
time v.voronoi -s input=myarea_general2000 output=skeleton_general2000 thin=2000
real 0m18.203s
user 0m17.988s
sys 0m0.196s
time v.voronoi -s input=myarea_general2000 output=centerline_general2000 thin=-1
real 0m18.029s
user 0m17.864s
sys 0m0.156s
Length of center line: 89468m
i.e. down to 18s, but now the results begin to differ significantly.
So first thing might be to simply recommend generalisation as a first step if approximation is acceptable.
Moritz
(attachments)